La geometría analítica estudia las figuras geométricas mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistemas de coordenadas Su desarrollo histórico comienza con la geometría cartesiana, impulsada con la aparición de la geometría diferencial de Carl Friedrish Gauss y más tarde con el desarrollo de la geometría algebraica. Actualmente la geometría analítica tiene múltiples aplicaciones más allá de las matemáticas y la ingeniería, pues forma parte ahora del trabajo de administradores para la planeación de estrategias y logística en la toma de decisiones.
Las dos cuestiones fundamentales de la geometría analítica son:
- Dado el lugar geométrico en un sistema de coordenadas, obtener su ecuación.
- Dada la ecuación en un sistema de coordenadas, determinar la gráfica o lugar geométrico de los puntos que verifican dicha ecuación.
Lo novedoso de la geometría analítica es que representa las figuras geométricas mediante fórmulas del tipo 
, donde 
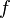es una función u otro tipo de expresión matemática: las rectas se expresan como ecuaciones polinómicas de grado 1 (por ejemplo, 
), las circunferencias y el resto de cónicas como ecuaciones polinómicas de grado 2 (la circunferencia 
, la hipérbola 
), etc.
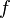, donde es una función u otro tipo de expresión matemática: las rectas se expresan como ecuaciones polinómicas de grado 1 (por ejemplo, ), las circunferencias y el resto de cónicas como ecuaciones polinómicas de grado 2 (la circunferencia , la hipérbola ), etc.
COORDENADAS
Las coordenadas cartesianas o coordenadas rectangulares son un ejemplo de coordenadas ortogonales usadas en espacios euclideos caracterizadas por la existencia de dos ejes perpendiculares entre sí que se cortan en un punto origen. Las coordenadas cartesianas se definen como la distancia al origen de las proyecciones ortogonales de un punto dado sobre cada uno de los ejes.
Las coordenadas cartesianas se usan por ejemplo para definir un sistema cartesiano o sistema de referencia respecto ya sea a un solo eje (linea recta), respecto a dos ejes (un plano) o respecto a tres ejes (en el espacio), perpendiculares entre sí (plano y espacio), que se cortan en un punto llamado origen de coordenadas. En el plano, las coordenadas cartesianas (o rectangulares) xe y se denominan abscisa y ordenada, respectivamente.
Se denominan coordenadas cartesianas en honor a Rene Descartes (1596-1650), el célebre filosofo y matemático francés que quiso fundamentar su pensamiento filosófico en el método de tomar un «punto de partida» evidente sobre el que edificaría todo el conocimiento.
Como creador de la geometría analítica, Descartes también comenzó tomando un «punto de partida» en esta disciplina, el sistema de referencia cartesiano, para poder representar la geometría plana, que usa sólo dos rectas perpendiculares entre sí que se cortan en un punto denominado «origen de coordenadas».
DISTANCIA ENTRE DOS PUNTOS
Para calcular la distancia d, se aplica el teorema de pitagoras. d es la hipotenusa del triangulo retangulo
La formula para resolver la distancia entre dos punto es la siguiente:
EJEMPLO
Supongamos que tenemos estos 2 puntos en el plano cartesiano u ortogonal.
A ( 2, 4 ) y B ( 3 , 6 )
Hallar la distancia entre esos puntos:
Entonces le damos nombre a esas coordenadas.
x₁ = 2
y₁ = 4
--
x₂ = 3
y₂ = 6
Empleando la fòrmula de la distancia entre 2 puntos:
d = √ (x₂ - x₁)² + (y₂ - y₁)²
Reemplazo el valor de cada nombresito que le pusimos
d = √ (3 - 2)² + (6 - 4)²
[Realizando lo que està dentro de parèntesis]
d = √ (1)² + (2)²
[Elevamos ambos tèrminos al cuadrado]
d = √ 1 + 4
d = √ 5
La distancia es la raiz de 5
Y el resultado es : 2. 236067 ...
Y eso es todo..
Resuelto.
En la siguiente pagina podrás practicar el manejo del plano cartesiano. Haz clic AQUÍ para ingresar.
No hay comentarios:
Publicar un comentario